How to Do Long Multiplication? Definition & Step-by-Step Guide
Do you think you could find the answer to 66 x 54? Multiplying big number can be challenging! But what if you didn’t have to multiply them on their own? What if there was a simple step-by-step process you could follow that will help you answer every equation that asks you to multiple two numbers that are larger than 10?
Well, there is!! It’s called the Long Multiplication Method.
The Long Multiplication method is a simple way to multiply large numbers. As long as you’re confident with your timetables, you’ll be tackling these sums in no time.
Knowing how to do Long Multiplication is important for the progress of Primary School students, as they begin to apply the basic principles of Mathematics to help them solve more complex problems.
What is Long Multiplication?
Long multiplication is a way to multiply large numbers by using the multiplication table. It helps us find the answer when multiplying numbers that are bigger than 10 and only requires basic multiplication knowledge.
Maths tutoring is available to those students who may need additional assistance with their Timetables, or for those who would benefit from one-on-one support as you try to understand the step-by-step Long Multiplication method.
Long Multiplication Step-by-Step
For our step-by-step guide on the Long Multiplication method, let us use 66 x 54 as an example.
For those of you who are visual learners, there is a visual example of each step provided.
For those of you who are aural learners, read this guide aloud to yourself, or to a tutor or parent/guardian.
Kinaesthetic learners would benefit from following along by visualising each step with a tutor or parent/guardian using objects found around the home.
Example: 66 x 54
- Write out the equation with the two numbers on top of each other. The larger number on the top and the smaller underneath it. Place the multiplication sign (x) to the left-hand side of the bottom number and draw a straight line underneath the equation. This stands for the = sign.
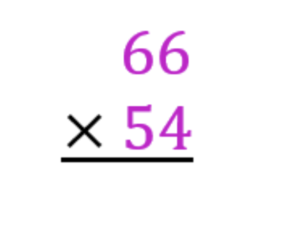
- Then, working from right-to-left, multiply the last digit of the bottom number with the last digit of the top number. In this case, the sum will be 6 x 4, which equals 24. This is a two-digit number. So put the 4 underneath, and carry the 2.

- Then multiply the last digit of the bottom number with the first digit of the top number. This again is 6 x 4. But this time, we have to add the number 2 remainder to the final answer. Think of it as 6 x 4 + 2. So instead of 24, the answer is 26.
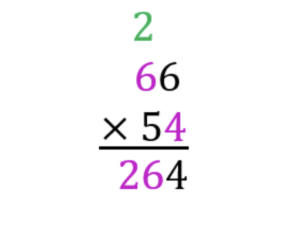
- Place a 0 below the answer, as shown. Then multiply the first digit of the bottom number with the second digit of the top number (5 x 6 = 30). Place the answer next to 0, and carry the 3.
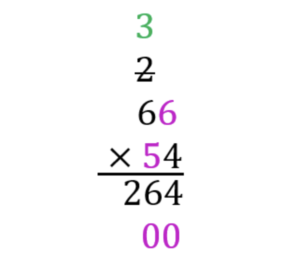
- As with step 3, now multiply the first digit of the bottom number with the first digit of the top number, remembering then to add the reminder number 3 to your answer. In this case, it will be 5 x 6 + 3 = 33. Add the answer.

- The final step is to then add together the two answers under the line. This will give you the final answer. In this example, you would use your knowledge of addition to solve 264 + 3300, which equals 3564.
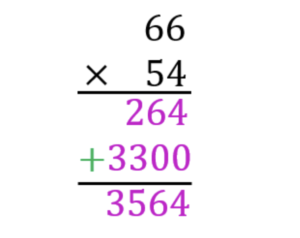
So, as you can see, you can use the Long Multiplication method, applying skills you have already learnt in Mathematics, to discover that 66 x 54 = 3564.
This step-by-step guide to Long Multiplication will work when multiplying any two numbers larger than 10. Even ones over 100!!
Long Multiplication Examples
Here are a few examples of long multiplication questions where you need to multiply numbers over ten:
- 43 x 25 =
- 123 x 18 =
- 340 x 98 =
- 357 x 103 =
- 2030 x 43 =
Try your best to use the Long Multiplication method to solve these equations. Once you have done so, use a calculator to see if you arrived at the correct answer!
Learning Long Multiplication Can Be Simple!
If you are faced with a multiplication equation that, on paper, looks complicated and overwhelming, the Long Multiplication method is your best friend.
Long Multiplication is a method of multiplying numbers larger than 10 that only needs your knowledge of the ten times Multiplication Table!
Above, you will find step-by-step instructions on how to solve such equations using the Long Multiplication method, alongside examples that you can use to practice your knowledge and skills.
Are you looking to improve your, or your child’s, maths grade but unsure where to start? A Team Tuition is here to help. Our tried and true tutoring methods can all students improve in any subject with our at-home and online tutoring services. Find a maths tutor near you today!
